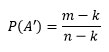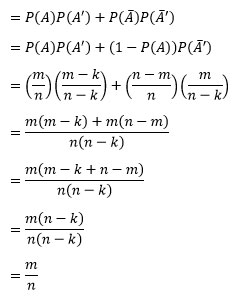Expected value of “Running it Twice”
First, let’s settle that running it twice (or any number of times) has the same expectation as running it once.
It is intuitive to deduce that the probability of the second run winning is equal to the first run. Simply recognize that the second run out doesn’t actually depend on the first (pretend as if the first run out is a set of exposed burn cards). Then the expected value for unit pot size is <P> = 0.5P1 + 0.5P2 where P1 = P2. Therefore, <P> = P1.
It is easy to fall into the trap of thinking that if you see the first run out, then the altered probabilities in the second run out yields a different expectation due to possible outs removed. Realize that you don’t see the cards from the first run out until after all the chips are in. This is different than seeing an exposed burn card when you have more decisions to make, knowing that card will never come up in both run outs if you ran it twice.
Mathematically, the probability of an event happening is between 0 and 1, or a fraction:
This means that over “n” trials, you would expect the event to occur “m” times. For poker, the likelihood of winning a pot is the same as saying we have “m” ways to win out of “n” possibilities.
Let’s assume the probability distribution A represents our chance of winning the pot in the first run out of cards.
If we win the first run out, when we remove the possibility and the equivalent winning possibility from the distribution, the probability of winning the next run out is slightly worse:
If we lost the first run out, the probability of winning the next trial is slightly better:
As a simple example where k = 1, let’s say you had 8 outs out of 40 cards by the river. and are running it twice.
If you won the first run out, you’d only have 7 outs out of 39 cards to win the second run out. You have one less winning possibility within the remaining distribution. Your probability of winning the second run out would be 7/39.
If you lost the first run out, you still have all 8 outs, but 39 cards left in the deck. In other words, you have one less losing possibility within the remaining distribution. Your probability of winning the second run out would be 8/39.
The total probability of winning the second run out is:
P(winning first run out) × P(winning with winning possibility removed) + P(losing first run out) × P(winning with losing possibility removed)
The probability of winning the second run out is the same as the first. The expectation of running it once is <P> = P × pot, and the expectation of running it twice is <P> = P × half-pot + P × half-pot. The expected values are the same.
For brevity, I won’t post the proof as to why removing the subset of winning possibilities due to card removal of a multiple card losing run out we would still arrive at the same conclusions. If we take a fraction of winning possibilities j (0 ≤ j ≤ 1) counted by “m” in the numerator, j × m, we would take a proportionate number of losing possibilities away from the total set counted by “n” in the denominator, j × (n – m) / m. Plugging in those values instead simplifies to the same results.
Maximizing PokerStars’ Card Match EV
PokerStars’ Card Match is another lottery-esque gimmick to divert rakeback from its traditional forms to an alternative form tailored towards “gambling rec’s” (recreational players). The idea is to match a set of individual cards with cards you hold in your hand over a series of deals. The cards qualify as a match only if you win or split the pot. Once you match all the cards within a certain number of hands, you are awarded a random bonus that is proportional to the limit you are playing (i.e. proportional to your rake contribution).
Splitting the pot is the key here to maximizing the efficiency in which you get the rakeback from Card Match. If you want to ensure you play the optimal minimum number of hands (for your style of play) to get the Card Match rakeback, you will want to enable the Run It Twice option so that you will qualify for matches maximally (by increasing the number of run outs seen relative to the number of deals since winning half-pots qualifies your hand for the promotion) without sacrificing EV. Ideally, you would stop playing immediately when you claim the prize until the next day you’re allowed to play Card Match again to maximize your expectation from it.
We’ve already concluded that running it twice has no effect on your EV whether you are a huge dog or favorite to win a hand before the board run outs, so you might as well reduce your variance with Run It Twice while increasing the efficiency of earning Card Match prizes.
* * *
If you appreciated the information in this article, consider a donation. You may also like gambling for fake money and for fun at GameSlush.